[学习笔记]计算机系统学习笔记Week1-2

信息的编码

机器级数据分为

​ 数值数据：无符号整数、带符号整数、浮点数

​ 非数值数据：逻辑数、西文字符和汉字

所有的信息都是使用二进制进行编码的

真值和机器数(重要!!!):
​ 机器数:用0和1编码的计算机内部的0/1序列
​ 真值：真正的值，即：现实中带正负号的数

数值数据表示的三要素

• 进位计数制
• 定、浮点数表示
• 如何用二进制编码

进位计数制

十进制、二进制、十六进制、八进制及其相互转换

定/浮点数表示(解决小数点问题)

• 定点整数、定点小数
• 浮点数(可用一个定点小数和一个定点整数来表示)

定点数的编码(解决正负号问题)

• 原码、补码、反码、移码

R进制计数制

R进制有R个基本符号(0~R-1),采用”逢R进一”的运算规则，对于每个数位i，该位上的权为Ri, R被称为该数字系统的基。

R进制表示法

二进制：Binary(以0b或者0B开头)

八进制：Octal(以”0”开头)

十进制：Decimal

十六进制：Hexadecimal(以”0x”开头或者以”H”为后缀)

十进制数与R进制数之间的转换

从低位到高位每3位二进制数可表示一位八进制数、每4位二进制数可表示一位十六进制数，高位补零

定点数和浮点数

定点数：小数点位置约定在固定位置的数称为定点数

浮点数：小数点位置约定为可浮动的数称为浮点数

​ 浮点数的尾数部分为定点小数，整数部分为带符号整数或者无符号整数

​ 任何实数X=(-1)S * M * RE,其中S取0/1，用来确定X的符号；M是一个二进制定点小数，称为X的尾数;E是一个二进制定点整数，称为X的阶或指数；R是基数。

原码、补码、反码、移码

原码的表示与机器数真值表示的一样，即用第一位表示符号(0为整数，1为负数)，其余位表示数值
如果用原码表示，让符号位也参与计算，对于减法来说，结果是不正确的。这也是计算机内部在存储数据时不使用原码的原因，为了解决这一问题，出现了反码。
反码的表示方法为：正数的反码是其原码本身。负数的反码是在其原码的基础上，符号位不变，其余各位取反
通过计算我们发现用反码计算减法，结果的真值部分是正确的。而唯一的问题出现在”0”这个特殊的数值上，虽然人们理解上**+0和-0**是一样的，但是0带符号是没有任何意义的，而且会有[0000 0000]原和[1000 0000]原两个编码表示0。为了解决这一问题，出现了补码。
补码的表示方法为正数的补码是其原码本身。负数的补码是在其原码的基础上，符号位不变，其余各位取反后加1（即在反码的基础上加1）。
为了方便浮点数进行加减运算时的对阶操作
移码的表示方法为将每一个数值加上一个偏置常数(Excess/bias)，通常当编码位数为n时，bias取2n-1或2n-1-1，当bias取2n-1时，移码为补码的高位加一。

补码-模运算

概念：在一个模运算系统中，一个数与它除以”模”后的余数等价
结论：

• 1、一个负数的补码等于**模减该负数的绝对值**
• 2、对于某一确定的模，某数减去小于模的另一数，总可以用该数加上另一数负数的补码来代替。

补码：[X]补=2n+X (-2n<=X <2n, mod 2n), X是真值，[X]补是机器数

变形补码

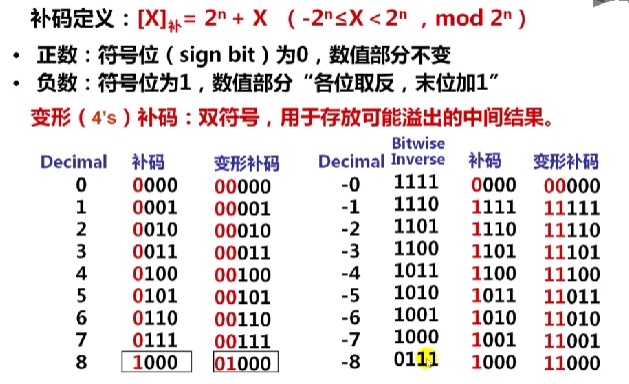
无符号整数

分为高到低位从左到右排列或从右到左排列，用LSB(Least Significant Bit)来表示最低有效位,用MSB来表示最高有效位，无符号位

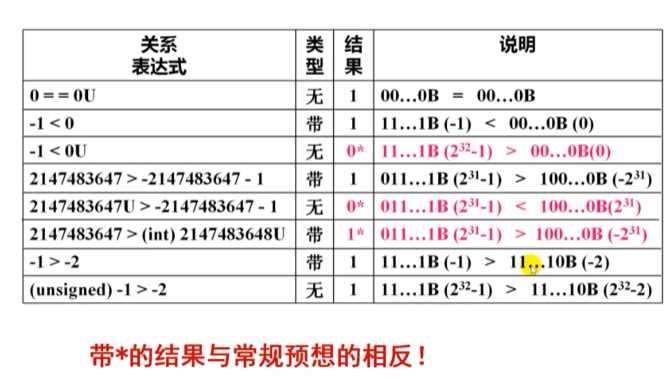
带符号整数

MSB为符号位，可用原码、移码、补码来表示

通常使用补码来表示带符号数：

​ 补码运算系统是模运算系统，加减运算统一

​ 数0的表示唯一，方便使用

​ 比原码多表示一个最小负数